At the end of previous chapter we have learn how to choose
among variety in programming languages. And we have preferred to use Python in
this course. But keep in mind, this course is not about Python. We use python
as a tools to present concept that related with computational problem solving
and thinking. There are many excellent online resources in the internet, that describing
almost every aspect of the language. Python features that we don't need for
that purpose are not presented at all.
“Since its introduction by Guido von Rossum in 1990, Python has
undergone many changes. For the first decade of its life, Python was a little
known and little used language. That changes with the arrival of Python 2.0 in
2000. In addition to incorporating a number of important improvements to the
language its self, it marked a shift in evolutionary path of the language. A
large number of people began developing libraries that interfaced seamlessly
with Python, and continuing support and development of the python ecosystem
became a community based activity. Python 3.0 was released at the end of 2008.
This version of Python cleaned up many of the inconsistencies in the design of
the various releases of Python 2 (often referred as Python 2.x). However, it
was not backward compatible. That means that most programs written for earlier
version of Python could not be run using implementation of Python 3.0.
The backward incompatibility presents a problem for this course. In our
view, Python 3.0 is clearly superior to Python 2.x. However, at the time of
this writing, some important Python libraries still do not work with Python 3.
We will, therefore, use Python 2.7 (into which many of the most important
features of Python 3 have been "back ported") throughout this course.“
- (Guttag, 2013)
The Basic Element of a
Program
A python program, sometimes called a script, is a sequence of definitions and commands are executed by
the Python interpreter in something called the shell. Typically, a new shell is
created whenever execution of a program begins. In most cases, a window is
associated with the shell. - (Guttag, 2013) . To have a bettter
understanding about a computer program, we have to look the basic element that
build a every good program. And here it is:
2.1 Statement/command
Sometimes computer didn’t have to make an operation and just
do a certain task, like printing something out, or take an input from an input
device or from another program. A command is an instruction given by a user
telling a computer to execute something, such a run a single program or a group
of linked programs. Commands are generally issued by typing them in at the
command line (i.e., the all-text display mode) and then pressing the ENTER key, (Command
Definition, 2004)
2.2 Object
Object are the core things that Python programs manipulate.
Every object has a type that defines the kinds of things that programs can do
with objects of that type. (Guttag, 2013) . Object have two characteristic, there
are states and behavior. For Example, aircraft can have state (position,
altitude, angle, engine thrust) and behavior (rolling, pull up, climbing, full
throttle). (Walrath, 1996) (Walrath, What Is an Object?,
1996)
As what we learn before that every object has a type. These
kind of types can be classified by two kind of object type, that are either scalar
or non-scalar. Scalar objects are indivisible, cause of each only have a single
value. Countrary with that, non-scalar objects that are divisible. For example,
17 as INT is a scalar object. In the other hand 17 as STR is a non-scalar
object because of it consist of 1 (STR) and 7 (STR). These are some example of
object types:
2.2.1 Object scalar
2.2.2 Object non scalar
2.3 Operator
Operator is about what computer will do with the object. As
we see in Chapter 1, each instruction build from operand and operator. So, all
programming languages will provide a set of operator, which generate generally
same behavior. Based on the expression, these operators can divide into 4 kind
of types:
2.3.1 Aritmatic operator
This type of operator is use when we want to calculate
something. When we use aritmatic operator, we will get aritmatic expression
|
Operator
|
Description
|
Example
|
|
+
|
Addition
- Adds values on either side of the operator
|
a + b
will give 30
|
|
-
|
Subtraction
- Subtracts right hand operand from left hand operand
|
a - b
will give -10
|
|
*
|
Multiplication
- Multiplies values on either side of the operator
|
a * b
will give 200
|
|
/
|
Division
- Divides left hand operand by right hand operand
|
b / a
will give 2
|
|
%
|
Modulus -
Divides left hand operand by right hand operand and returns remainder
|
b % a
will give 0
|
|
**
|
Exponent
- Performs exponential (power) calculation on operators
|
a**b will
give 10 to the power 20
|
|
//
|
Floor
Division - The division of operands where the result is the quotient in which
the digits after the decimal point are removed.
|
9//2 is
equal to 4
and
9.0//2.0 is equal to 4.0
|
2.3.2 Comparison operator
When we want to know about something and how it’s value or
property, we usually compare it with an object that has a known value or
object. It is like when we use ‘meter (m)’ as a base unit to evaluate length of
a box.
* Remember to only compare two object that has the same
type.
|
Operator
|
Description
|
Example
|
|
==
|
Checks if
the value of two operands are equal or not, if yes then condition becomes
true.
|
(a == b)
is not true.
|
|
!=
|
Checks if
the value of two operands are equal or not, if values are not equal then
condition becomes true.
|
(a != b)
is true.
|
|
<>
|
Checks if
the value of two operands are equal or not, if values are not equal then
condition becomes true.
|
(a
<> b) is true. This is similar to != operator.
|
|
>
|
Checks if
the value of left operand is greater than the value of right operand, if yes
then condition becomes true.
|
(a >
b) is not true.
|
|
<
|
Checks if
the value of left operand is less than the value of right operand, if yes
then condition becomes true.
|
(a <
b) is true.
|
|
>=
|
Checks if
the value of left operand is greater than or equal to the value of right
operand, if yes then condition becomes true.
|
(a >=
b) is not true.
|
|
<=
|
Checks if
the value of left operand is less than or equal to the value of right
operand, if yes then condition becomes true.
|
(a <=
b) is true.
|
2.3.3 Logic operator
We use logic operator when we want computer to think like us.
There only two main kind of logic operator that are:
-
AND operator
-
OR operator
With this operator we can tell computer to use all the
expression that allowed and provide us a conclusion.
2.3.4 Assignment operator
After make a conclusion, usually, we want to assign a
computer object to do or get something. For this, we will use assignment
operator as following:
|
Operator
|
Description
|
Example
|
|
=
|
Simple
assignment operator, Assigns values from right side operands to left side
operand
|
c = a + b
will assigne value of a + b into c
|
|
+=
|
Add AND
assignment operator, It adds right operand to the left operand and assign the
result to left operand
|
c += a is
equivalent to c = c + a
|
|
-=
|
Subtract
AND assignment operator, It subtracts right operand from the left operand and
assign the result to left operand
|
c -= a is
equivalent to c = c - a
|
|
*=
|
Multiply
AND assignment operator, It multiplies right operand with the left operand
and assign the result to left operand
|
c *= a is
equivalent to c = c * a
|
|
/=
|
Divide
AND assignment operator, It divides left operand with the right operand and
assign the result to left operand
|
c /= a is
equivalent to c = c / a
|
|
%=
|
Modulus
AND assignment operator, It takes modulus using two operands and assign the
result to left operand
|
c %= a is
equivalent to c = c % a
|
|
**=
|
Exponent
AND assignment operator, Performs exponential (power) calculation on
operators and assign value to the left operand
|
c **= a
is equivalent to c = c ** a
|
|
//=
|
Floor
Dividion and assigns a value, Performs floor division on operators and assign
value to the left operand
|
c //= a
is equivalent to c = c // a
|
2.4 Expression
In simple way expression is a type of instruction that we
make when we combine object (operand) with operator, which denote an object of
a type. That why, every expression consists of at least one operand and can
have one or more operators. For example, in the C language x+5 is an
expression, as is the character string "MONKEYS." From expression we
can get instruction (See section 1.2.1). An instruction can build by a single
expression or from many of it. Example, when we use looping we need to
expression to compare each other.
In programming, an expression is any legal combination of operand
(object) and operator that have a value. Each programming language and
application has its own rules for what is legal and illegal. I suggest to see
again section 1.6.
Expressions are often classified by the type of operand or
object that they represent. For example:
- § Boolean expressions: Evaluate to either TRUE or FALSE
- § Integer expressions: Evaluate to whole numbers, like 3 or 100
- § Floating-point expressions: Evaluate to real numbers, like 3.141 or -0.005
- § String expressions: Evaluate to character strings
2.5 Variable
Every program language has a different meaning for variable.
In Python a variable just a name for an object. We use an assignment operator
to combine and object with variable. An object can have one or more than one
name that associated with it. Example:
Pi = 3.14159
Phi = 3.14159
Those two expression is an example of naming floating object
3.14159 with variable Pi and Phi.
In Python, variable names can contain letter, digits &
special character _. Python variable name are also case-sensitive. There are a
small number of reserved keywords in python that have built-in meaning and
cannot be used as variable names. Those word are usually have been used as
command or statement. Example in Python 2.7 are and class, del, pass,
print, while, etc. (Guttag, 2013)
2.6 Comment
Purpose of a comment is to make a program easy to read (by
programmer). Comment will helps programmer to produce a well form program. Not
to explain the language or the semantics but to explain the thinking behind the
program or to explain the algorithm. So we suggest to assume the reader
understand the language.
2.7 Branching program
The kind of computation we have been looking at this far are
called straight-line program. They execute one statement after another in the
order in which they appear, and stop when they run out of statements. These
kind of programs aren't very interesting. In fact, they are downright boring. (Guttag, 2013)
There are three way to branching a program.
2.7.1 Conditional (If …)
The simplest statement to branching a program is to use a
conditional. A conditional statement
usually has three part:
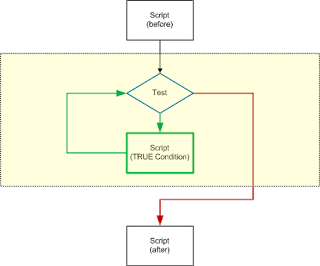
Figure 2.1 - Conditional
Branching Program
a. a test, i.e., an expression that evaluates to
eather true or false;
b. a block of code that is executed if the test
evaluates to True; and
c. an optional block of code that is executed if the test
evaluates to false.
Becarefull!!! In python indentation is a semantically
meaningfull.
2.7.2 Looping or iteration
A generic iteration mechanism is depict in figure .... Like
a conditional statement, it begins with a test. If the test evaluate to true,
the program execute the loop body once, and then goes back to reevaluate the
test. this process repeat until the test evaluates to False, after which
control passes the code following the iteration statement.
Figure 2.2 -
Iteration Branching Program
There are two type of statement in iteration, that are:
2.7.2.1 Countable Looping (For …)
Executes a piece of script multiple times and abbreviates
the code that manages the loop variable. (tutorialspoint.com) The number of repetition
determined by the program or the user.
The loop "counts" the number of times the body will be
executed. This loop is a good choice
when the number of repetitions is known, or can be supplied by the user. (mathbits.com)
2.7.2.2 Conditional Looping (While …)
Repeats a statement or group of statements while a given
condition is TRUE. It tests the condition before executing the loop body. (tutorialspoint.com) If the
"condition" is FALSE at the beginning of the loop, the loop is never
executed. The "condition" may
be determined by the user at the keyboard.
The "condition" may be a numeric or an alphanumeric entry. (mathbits.com) This is a good, when we focus on the “condition”,
and we don’t care about the number of repetition.
2.7.3 Steps Jumping
2.7.3.1 (Jump … / Go To…)
This is the simplest statement to jumping from one sequence of
statement to another.
2.7.3.2 Function / subroutine
We will discusses this in a chapter, later.
Bibliography
Command Definition. (2004, June 15). Retrieved August 27, 2014, from www.linfo.org:
http://www.linfo.org/command.html
Expression. (n.d.). Retrieved
12 04, 2015, from www.webopedia.com:
http://www.webopedia.com/TERM/E/expression.html
Guttag, J. V. (2013). Introduction to Computation and Programming
Using Python (spring 2013 ed.). Cambridge, Massachusetts: The MIT Press.
Mathbits.com. (n.d.). Which LOOP should I use???? Retrieved
January 9, 2016, from http://mathbits.com:
http://mathbits.com/MathBits/CompSci/looping/whichloop.htm
Tutorialspoint.com. (n.d.). Python Loops. Retrieved January 9,
2016, from http://www.tutorialspoint.com:
http://www.tutorialspoint.com/python/python_loops.htm
Walrath, M. C. (1996). The Java Tutorial - Object-Oriented Programming
for the Internet. Addison-Wesley Pub.
Walrath, M. C. (1996,
August). What Is an Object? Retrieved December 2014, from
http://journals.ecs.soton.ac.uk/:
http://journals.ecs.soton.ac.uk/java/tutorial/java/objects/object.html